Calcudoku Solving Strategies
Our calcudoku puzzle magazine contains 100 calcudoku puzzles (funnily enough), but if you're not too sure how to play the puzzle then have a quick read through these calcudoku hints and tips before tackling the puzzles.
First, a reminder of the rules. Calcudoku come in a range of sizes and if you've not come across that name before, it is also published under names such as hitoshii and kenken, however kenken is a trademark and therefore other publishers do not use this name; calcudoku seems to be the standard name that it is permissible for everyone to use. All our calcudokus are 6x6 in size. You must place 1 - 6 in each row and column and into the bold lined regions such that the total of each bold lined regions matches the sum at the start of the region. With division and subtraction sums, you must divide or subtract each number (or the numbers) in a region from the largest number. You may repeat a number within a bold lined region as long as it does not break the rule that 1 - 6 must occur just once in each row and column.
If you are coming to the puzzle from killer sudoku, then the repetition may confuse you at first. The bold regions that are in a straight line and all in one row or column as a result have less options as they cannot contain repetition and therefore you might like to look at these first. As with killer sudoku, looking for unique combinations is the best way to progress at speed.
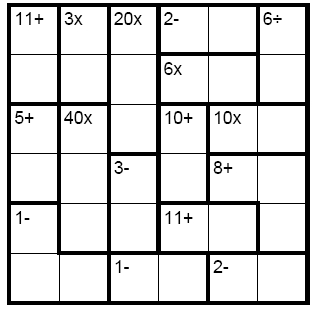
As with killer sudoku, you will frequently use the fact that you don't know exactly what value a cell contains but know it must be one of, say, two, to eliminate the options from other cells. Let's look at the sample puzzle to the right. Now, scan for unique combinations. Well, we know that the '6/' at the top right of the grid (cells R1C6, or row one column six, and R2C6) must be 1 and 6 in some order because that's the only possible sum that gives a result of 6 with those two values. Therefore we know that the rest of column six cannot contain 1 or 6.
In this simple puzzle, there are many instances where we can use this logic. Look at the '11+' in R5C4 and R5C5. This must be 6,5 in some combinations, and the '10x' in R3C5 and R3C6 must be 2,5 in some order. The key is to use this information to eliminate values from other regions until you can definitely place a number.
Look at column two. The first sum is '3x' which we know must be 1,3 in some order. Then there is a '40x' which we know must be composed out of three of 2,4,5,6. Well, we know that 6 is not a factor of 40 (40 divided by 6 is not an integer) and therefore we know that it cannot contain a 6. Therefore it must be 2,4,5 in some order. This leaves only one place in the region that the 6 can go: that's it's final cell, R6C2, and so we can place a '6' in that cell. Definitive progress! And in fact since we've already worked out that cells R3C5 and R3C6 contain 2 and 5, we can place the 4 in R3C2 at the top of the '40x' box.
And that's how to go about solving calcudoku puzzles: simply look carefully at the possible valid combinations for each region, and how these restrict the possible combinations for other regions. By diligently applying this method throughout the puzzle you will be able to solve the majority of calcudoku puzzles. There are other harder methods that can be used to, and you may discover these whilst solving the puzzles. Just take care to remember that values can repeat in regions that are spread across more than one row/column!
And remember one advantage of those regions with repetition is that sometimes they can be placed instantly before anything else is written in the grid because they have a unique order as well as a unique combination. For instance, imagine that the '1-' at the bottom left of this grid was actually '2x'. Well, we would be able to write in the precise combination as there is only one that fits, nevermind pencilmarks as with the previous regions we've looked at! It must be precisely 1,2,1 with the '2' in R6C1 and the other two cells containing 1, as any other combination would break the constraint that a number cannot be repeated in a row or column.
So those are the hints on tackling calcudoku; now why not download the calcudoku puzzle magazine and enjoy 100 puzzles!
Read more Puzzle Strategy Tips on a range of different puzzle types.
Prefer books to PDF magazines? Our books make great gifts for any puzzle fans:
Crossword a Day 2025 |
Kriss Kross a Day 2025 |
Sudoku a Day 2025 |
Codeword a Day 2025 |
| Check out the full PUZZLE A DAY 2025 range of books >>> | |||
