Solving Consecutive Sudoku
 If you have either purchased the consecutive sudoku magazine or are simply tackling the puzzles from the sample page and are unsure how to play, here we look at the strategy of this interesting looking variant on sudoku in more detail.
If you have either purchased the consecutive sudoku magazine or are simply tackling the puzzles from the sample page and are unsure how to play, here we look at the strategy of this interesting looking variant on sudoku in more detail.
First things first. The usual rules you are familiar with of placing 1 - 9 in each row, column and 3x3 box apply so never forget that as you'll need to use that information many times whilst solving the puzzles, either independently of the consecutive rule or, well, consecutively with it.
The rules of the game dictate that the little grey rectangles that sit between cells tell you that the values of those cells are adjacent. If one contains a 1, the other must be a 2. If one contains a 9, the other must be an 8. Other than that, there will be two possible values where one is known. Thus if one contains 2, the neighbour must be 1 or 3. Of course, if either of those is already eliminated in a region in which the second cell is in, then there is only one candidate that can be written straight in.
So far with our solving strategy tips for consecutive sudoku magazine, things have been quite straightforward. And indeed the logic for solving these puzzles is not hard. But sometimes you will need to work through a series, or chain of consecutive values, possibly with little information known, and it is here that things can get quite interesting as a series of values can ripple through the cells with interesting effects and surprising deductions possible from the amount of information made available from a run of consecutive cells that may not be immediately apparent.
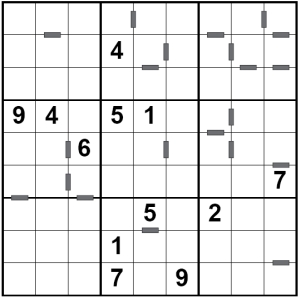
Many puzzles have a couple of 'freebies' you can write straight in. Looking at the first puzzle from the magazine, to the right, then you can see in row 5, column 9, the value can be written straight in. Can you see what it is and why? That's the key to using the consecutive information to solve the puzzles.
You will also need to use sets in a fairly simple fashion in these puzzles, but applying them to the consecutive regions can be tricky as you'll need to take care to make all the deductions possible without slipping up.
Let's look at squeezing the most information we can from the consecutive information right at the start. Look carefully at row 4, cell 7. Now, a quick scan of the grid tells us that 1, 2, 4, 5, 7, 9 are already in the row, column and box that cell is in. This leaves us with 3, 6 and 8 left to place.
However, we can place '3' straight off *AND* the values of the cell to the left and below R4C7 using the power of consecutive regions! The cell cannot contain 6, because it is consecutive in value to the cell to its left and the cell below, both of which are in the same region and therefore cannot be the same value. This means that if R4C7 is 6, then one of the neighbours must be 7, but there is already a 7 in this region. So 6 is removed as a candidate. Exactly the same logic applies to the 8. This just leaves the 3, which we can place in R4C7, with the 4 in the cell beneath it and 2 in the cell to its right. It is simple but not immediately obvious logic like this that is the key to solving consecutive puzzles successfully.
Now you know how to do it, why not buy consecutive sudoku magazine and enjoy solving these fascinating but rare sudoku variant puzzles with the many subtle and interesting logical rules that can be used to solve them?
Read more Puzzle Strategy Tips on a range of different puzzle types.
Prefer books to PDF magazines? Our books make great gifts for any puzzle fans:

Sudoku a Day 2026 |

Kriss Kross a Day 2026 |

Codeword a Day 2026 |

Crossword a Day 2026 |
| Check out the full PUZZLE A DAY 2026 range of books >>> | |||







